当深入推理模型DeepSeek-R1、OpenAI o1等仍然通过增加推理计算量来提高性能时，California University of Berkeley和Allen Artificial Intelligence Institute突然抛出了一个深水炸弹：让推理模型不再需要显式token卷积，无需明确的思维链，就能实现高效且准确的推理。

这项研究认为显式思考过程将会明显增加 token 使用量和延迟，从而导致推理效率下降。

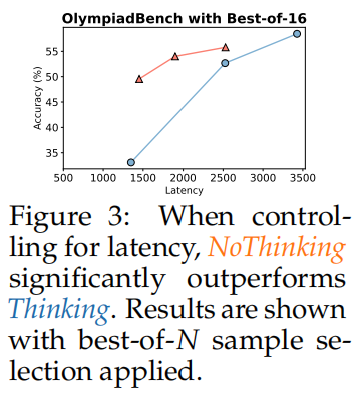
在控制延迟条件时，NoThinking的效果显著优于Thinking。

这项研究的出人意料的结论吸引了不少眼球。例如，亚马逊研究多模态 LLM 的博士后 Gabriele Berton总结说，NoThinking 方法的本质上就是强制模型输出：「思考：好了，我已经思考完了。」

请提供原文，我将对其进行语言润色。

与 Thinking 相比,NoThinking 能更好地权衡精度与预算的关系。

在现代社会中，我们渐渐地发现，人类的思想模式正经历着一个深刻的转变。随着技术的不断发展和数字化的生活方式，我们的思想方式开始从传统的线性思维转变为更加非线性的、更加灵活的思考方式。这种新的思想模式称为"Thinking"（思考）. Thinking 是一种能够不断地探索、分析和解决问题的思想方式，它能够帮助我们更好地适应不断变化的环境和挑战。Thinking 可以使我们更好地理解复杂的关系和问题，并且能够激发我们的创造力和创新精神. 然而，另一种思想模式却是不同的。这种思想模式称为"NoThinking"（不思考）。NoThinking 是一种避免思考、避免思考的思想方式，它通常是由于恐惧、疲惫或其他原因所致的。NoThinking 可以使我们感到压力和疲惫，并且可能会导致我们错过了很多有价值的机会和经验. 因此，我们可以看到，Thinking 和 NoThinking 是两个截然不同的思想模式，它们对我们的人生和思想都有着深远的影响。

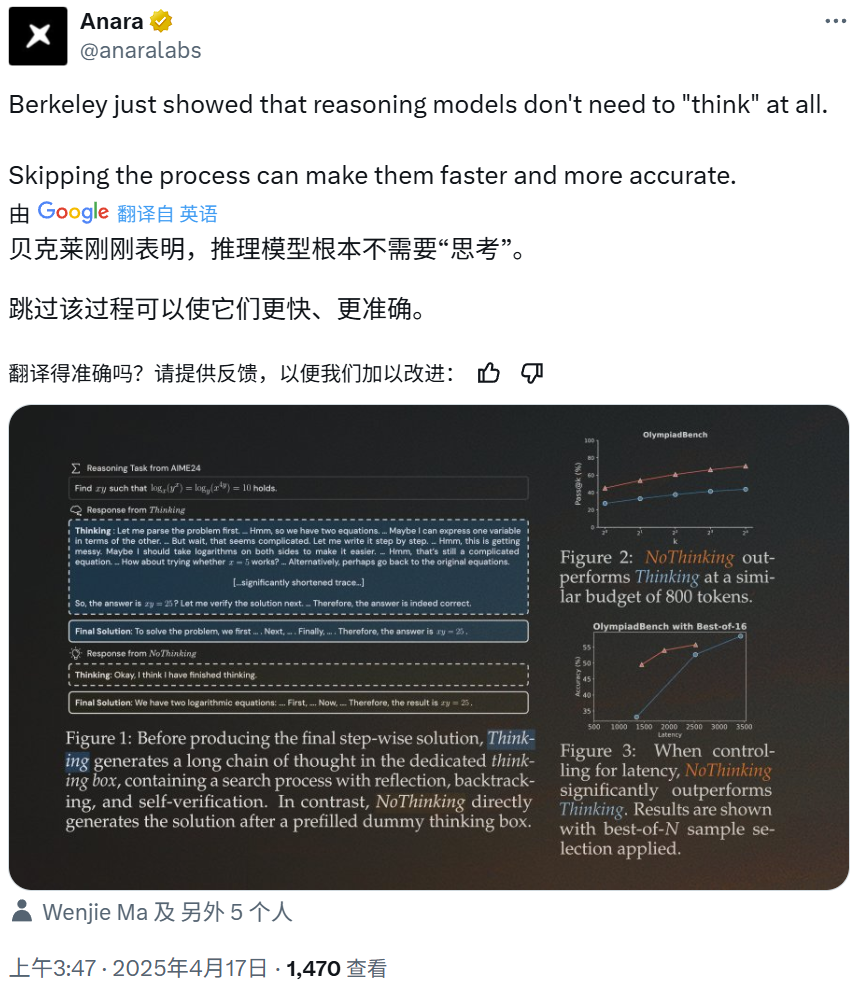
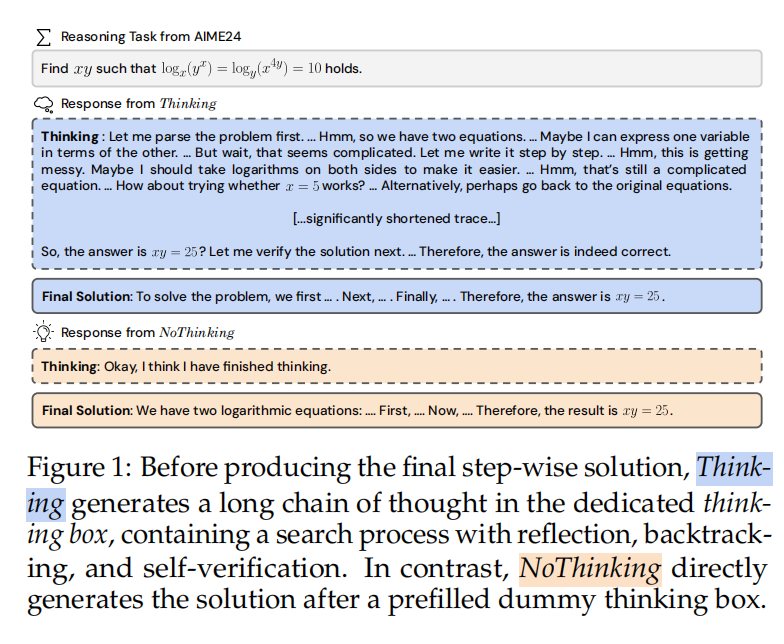
大多数现代推理模型，如 R1 和 R1-Distill-Qwen，在其生成过程中都遵循类似的结构：在思考框内的推理过程，以"<|beginning_of_thinking|>"和"<|end_of_thinking|>"为标志，然后是最终答案。基于这种结构，将两种方法（Thinking 和 NoThinking）定义如下：

思考指的是查询推理模型以生成以下输出的默认方法：在思考框内的推理过程、最终解决方案和最终答案（图1中的蓝色）。

"NoThinking" 指的是通过提示绕过显式推理过程，直接生成最终解决方案和答案的方法。这一方法可以通过在解码过程中强制思维框为空来实现，如下所示。

<|beginning_of_thinking|>我认为我已经完成思考。<|end_of_thinking|>

为了控制两种方法中的token使用量，当模型达到token预算时，它将被迫生成「最终答案」，以确保立即得到最终答案。如果模型在达到token限制时仍在思考中，<|end_of_thinking|>将附加在最终答案标签之前，以提示用户模型已经达到token限制。

以精准的实验设置为基础，科学家们将对某种新的材料进行复杂的测试和分析。

基于深度探索 R1 的蒸馏版本，DeepSeek-R1-Distill-Qwen-32B 作为主要模型，通过使用 Qwen-32B 初始化模型，并在深度探索 R1 生成的数据上进行训练，创建了该模型。据报告，这是使用顺序测试时间扩展的一种最先进推理模型之一，与规模更大的 DeepSeek R1-Distill-Llama-70B 相媲美。

还提供了一系列具有挑战性的推理基准，包括数学竞赛、编码、奥林匹克竞赛问题和定理证明等任务，旨在考验学生的逻辑思维和解决问题的能力。其中，以多样本准确率（pass@k）为指标，它衡量的是在每个问题所生成的 n 个完整回复中，随机选取 k 个样本，其中至少有一个正确输出的概率。

其形式化定义为：以数学逻辑为基础的概念系统，旨在描述语言的语义结构和语法规则。

其中 n 是每个问题的采样输出数量，c 是正确输出的数量。

根据标准，对定理证明数据集（MiniF2F 和 ProofNet）使用 k = {1, 2, 4, 8, 16, 32}；对于较小的数据集（2024 年美国数学邀请赛、2025 年美国数学邀请赛、2023 年美国数学竞赛），k = {1, 2, 4, 8, 16, 32, 64}；对于较大的数据集（奥林匹克竞赛基准测试、实时编码基准测试），k = {1, 2, 4, 8, 16}。对于形式定理证明基准测试，“多样本准确率（pass@32）”是标准指标，而对于数学和编程基准测试，最常用的是“单样本准确率（pass@1）”（即准确率）。

实验结果表明，新的材料具有显著的改善性能，能够更好地适应复杂的应用场景。

在未控制 token 预算的情况下对 Thinking、NoThinking 与 Qwen Instruct 进行对比，发现这三个模型在处理语言理解和生成任务方面存在明显的差异。Thinking 模型的优势在于其能够更好地捕捉语言的语义和上下文信息，从而生成更加合理和有意义的文本。相比之下，NoThinking 模型的性能较差，它可能会生成一些不相关或不合理的文本。Qwen Instruct 模型则在中间位置，它能够生成一些有意义的文本，但其性能也存在一定的不确定性。总的来说，这三个模型在未控制 token 预算的情况下都存在一定的局限性，但 Thinking 模型在语言理解和生成任务方面的性能最为出色。

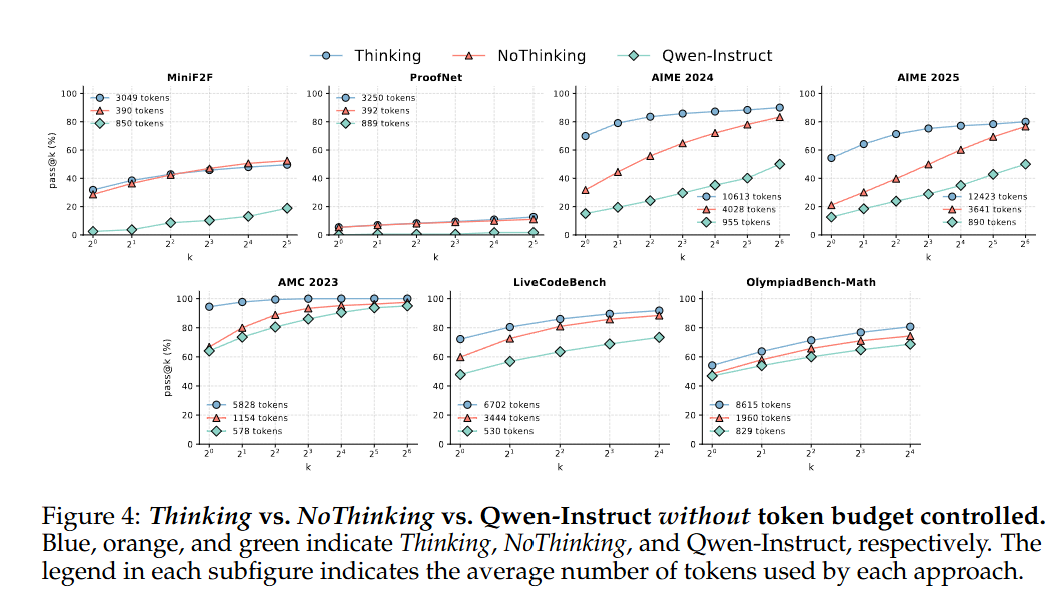
首先，在MiniF2F和ProofNet上，NoThinking在所有k值上的表现与Thinking相等，两者都显示出明显的优越性，特别是考虑到NoThinking使用的token比Thinking少3.3-3.7倍，这一结果尤其让人感到惊讶。在其他数据集上，结果则变得更加复杂。在k=1时，NoThinking落后于Thinking，但随着k的增加，差距逐渐缩小。

在所有数据集中，当 k 值达到最大时，NoThinking 的表现与 Thinking 相当，但 token 使用量却明显低于 Thinking，具体来说是 2.0-5.1 倍。在 AIME24、AIME25 和 LiveCodeBench 上，Thinking 和 NoThinking 都具有明显的优势，显著优于 Qwen-Instruct。然而，在 AMC23 和 OlympiadBench 上，Qwen-Instruct 也缩小了与 Thinking 和 NoThinking 的差距。

在 token 预算控制下的情况下，Thinking 和 NoThinking 之间的对比显示出明显的差异。

除MiniF2F和ProofNet外,NoThinking在其他数据集上的表现虽然略逊于Thinking，但其token消耗量也明显更低。

因此，接下来继续通过预算约束方法，来评估在相近token预算下的两者的性能表现。

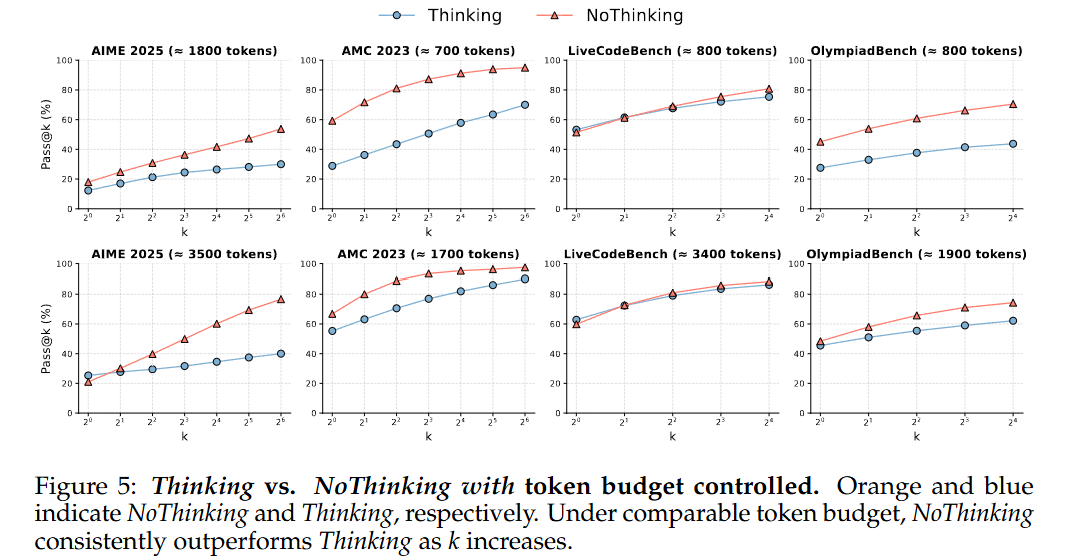
如图 5 所示，当 Token 使用量受到控制时，NoThinking 方法通常优于 Thinking 方法。特别是在低预算设置下（例如，使用的 Token 数少于约 3000 个），在所有的 K 值情况下，NoThinking 方法始终取得更好的结果，并且随着 K 值的增加，性能差距会进一步扩大。当 Token 使用量较高时（例如，大约 3500 个 Token），在单样本准确率（Pass@1）方面，Thinking 方法的表现优于 NoThinking 方法，但从 K = 2 开始，NoThinking 方法的表现就迅速超过了 Thinking 方法。

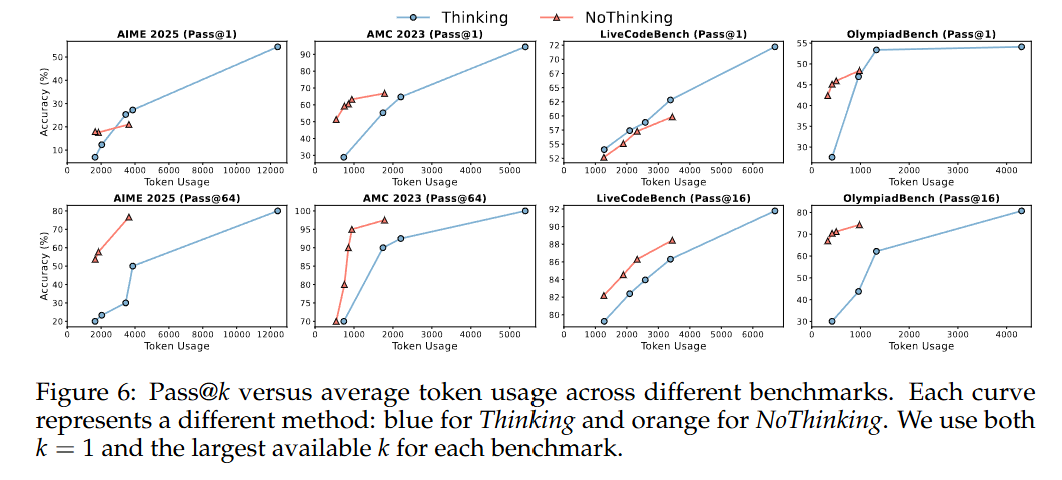
根据 token 使用量的横轴绘制，进一步证实了这些结果，同时对比了单样本准确率（pass@1）和在可用最大 k 值下的多样本准确率（pass@k）。结果表明，NoThinking 方法在整个预算范围内始终保持优势，始终优于 Thinking 方法。在单样本准确率（pass@1）方面，NoThinking 方法在低预算情况下表现更好，而在高预算情况下则出现了下降。然而，实时编码基准测试是一个例外，在该基准测试中，即使是在低预算情况下，Thinking 方法在单样本准确率（pass@1）方面也优于 NoThinking 方法，这可能是因为禁用思考模块在实时编码基准测试上并不能显著减少 token 使用量。

为了降低数据污染的风险，实验还纳入了新发布的AIME 2025，这些数据不太可能出现在现有模型的预训练数据中。值得注意的是，在新的基准测试和已有的基准测试中都获得了一致的结果，这明确表明研究所观察到的趋势并非是模型记忆的产物，而是反映了模型具有可泛化的行为表现。

对 NoThinking 方法的性能产生了显著影响。随着 k 值的增加，方法的计算复杂度和时间复杂度也相应增加。这是因为 k 值的增加导致了 Hash 表的大小和 Hash 函数的计算复杂度的增加，从而影响了方法的执行效率。

该团队研究了随着 k 值增加，所观察到的 NoThinking 方法性能变化的潜在原因，他们专注于探究生成答案的多样性。这是通过计算每个问题的答案分布熵来衡量的。具体来说，对于答案分布为...

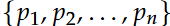
熵的定义为：熵是指系统中的无序度或 randomness，衡量系统中信息的混乱程度或不确定性。

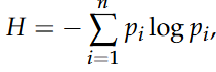
以下是润色后的内容： 其中，p_i是第i个独特答案的经验概率。为了总结多样性，使用了所有问题的熵的均值和标准差进行分析。均值熵的高值表明总体多样性较大，而标准差的低值则意味着各个问题之间的多样性更为一致。这些分析基于图5中Thinking方法与NoThinking方法的对比情况，但不包括缺少确切答案的实时编码基准测试。

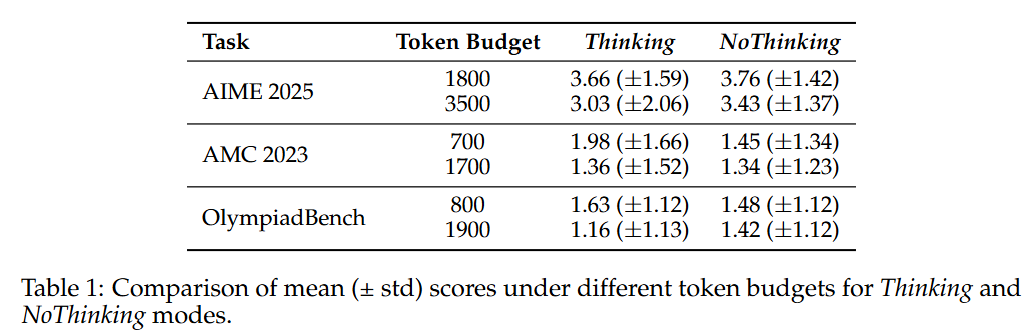
从表1可以看到，两种模式在平均多样性方面都没有明显的优势。有时候，NoThinking模式的平均熵会更高，而在其他情况下，Thinking模式的平均熵会更高。然而，NoThinking模式始终在每个问题上表现出更低的方差，这表明NoThinking模式生成的答案在不同示例之间具有更均匀的多样性。研究者们认为，这种多样性一致性的提高可能是NoThinking模式在多样本准确率（pass@k）上的性能提升的原因之一，尽管仅靠多样性无法完全解释性能差异。

NoThinking 方法使测试阶段的并行计算更加高效。

并行scaling和顺序scaling是两个关键的技术概念，用于提高计算机系统的性能和效率。并行scaling是指在多个处理器或核心上同时执行多个任务，以充分利用系统的计算资源。顺序scaling是指在单个处理器或核心上逐个执行多个任务，以提高系统的计算速度和效率。

并行 scaling 的本质在于能够实现低延迟，因为多个模型调用可以同时执行，无论是通过应用程序编程接口的调用还是本地模型服务的实现。这可以通过多 GPU 设置或在单个 GPU 上进行批处理来达成，与顺序 scaling 相比，这种方式能够实现更高的 GPU 利用率。总体延迟由单个最长的生成时间决定。

鉴于实验发现，NoThinking 方法在低预算情况下能够生成更准确的解决方案，且随着k值的增加，在多样本准确率（pass@k）方面的效果日益显著。这进一步证实了，当NoThinking方法与简单的「从N个中选最佳（Best-of-N）」方法相结合时，采用并行采样的NoThinking方法能够显著提高准确率。相比之下，在延迟相当的情况下，它的表现优于其他方法，例如采用强制预算和并行采样的Thinking方法。即使其产生的延迟要低得多，但它甚至在顺序 scaling 的情况下超过了完整Thinking方法（即不采用强制预算的Thinking方法）的单样本准确率（pass@1）性能。

请提供待润色段落的内容，我将对其进行语言润色，提升表达质量。

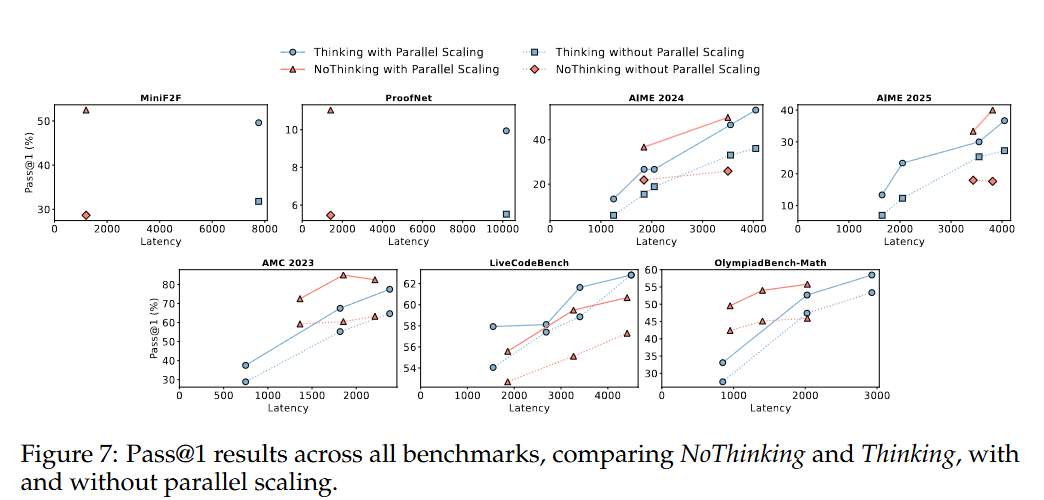
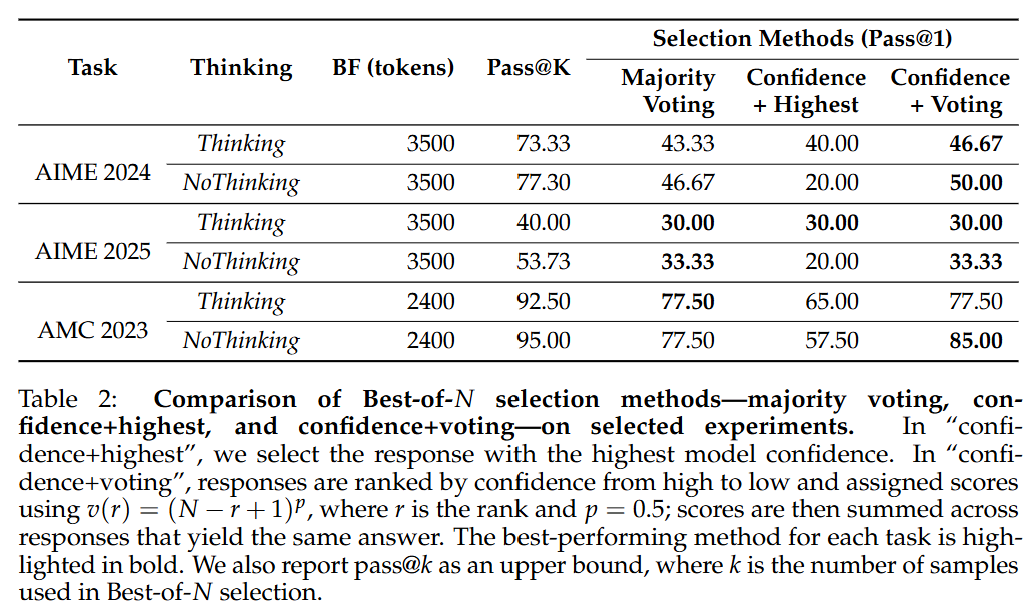
图 7 中展示了 Thinking 方法和 NoThinking 方法在所有基准测试中的单样本准确率（pass@1）结果，该准确率衡量了单个采样响应的性能在无并行 scaling 情况下的表现。相对地，对于多个样本进行「从 N 个中选最佳」选择后的准确率则被视为有并行 scaling 情况下的单样本准确率（pass@1）。在没有验证器的任务中，我们使用基于置信度的结果，并在表 2 中提供了选定实验的消融实验结果，以比较「从 N 个中选最佳」方法的性能。此外，我们还报告了多样本准确率（pass@k），将其视为使用并行 scaling 时单样本准确率（pass@1）的上限，表明基于置信度的选择方法通常优于多数投票法。

NoThinking 方法与并行 scaling 相结合，为传统的顺序方法提供了一种高效的替代方案，能够在显著降低延迟和 token 使用量的情况下，达到相似甚至更好的准确率。如图 7 的前两个图所示，NoThinking 方法实现了与 Thinking 方法相当甚至更高的性能，同时延迟要低得多。在没有并行 scaling 的情况下，NoThinking 方法在准确率上与 Thinking 方法相近，而延迟仅为后者的一小部分。

如果有一个完美的验证器可用，那么从 k 个采样响应中选择最佳的一个就能实现 pass@k 准确度。使用 NoThinking 方法，可以在准确率上与不采用强制预算且不进行并行 scaling 的 Thinking 方法相当，同时将延迟降低到原来的七分之一。更值得注意的是，在 MiniF2F 和 ProofNet 这两个数据集上，NoThinking 方法使用的输出 token 数量减少了四分之三，却实现了相同的准确率，这凸显了它的计算效率。这些结果强调了在有验证器可用的情况下，并行采样的有效性。

当 NoThinking 方法与并行 scaling 以及基于置信度的选择方法相结合时，在大多数基准测试中，它在低 token 预算的情况下始终优于 Thinking 方法。图 7（最后五个图）展示了基于置信度选择方法在多个基准测试中的结果，比较了在受控 token 使用量情况下 Thinking 方法和 NoThinking 方法的表现。

关注低预算情况有两个原因：一是，这符合我们对高效推理的主要研究兴趣；二是，如果将最大 token 数设置得过高，通常会导致输出内容过长且不连贯（「胡言乱语」），这会增加延迟并降低比较的价值。

正如预期那样，并行 scaling 提高了 Thinking 方法和 NoThinking 方法的单样本准确率（pass@1）性能。然而，在所有数学基准测试中，NoThinking 方法始终占据着帕累托最优边界的主导地位。

在并行 Scaling 的 Thinking 方法方面，NoThinking 方法展现出更优的准确率与预算之间的权衡效果。在 AMC 2023 和 OlympiadBench 基准测试中，无论是否采用并行 Scaling，NoThinking 方法的表现始终优于 Thinking 方法。值得注意的是，即使与完整的 Thinking 方法（不采用强制预算的 Thinking 方法）相比，NoThinking 方法能够将延迟降低到原来的九分之一，同时还实现了更高的单样本准确率（pass@1）得分，达到了 55.79 compared to 54.1。

NoThinking 方法在 LiveCodeBench 上的效果较差，该基准测试似乎是个例外情况。这可能是因为基于置信度的选择方法在编码任务中存在局限性，在没有完全匹配输出的情况下，投票策略无法应用。在这种情况下，只能退而求其次，选择置信度最高的答案，而这种方式的可靠性较低。如表 2 所示，与在可应用投票策略的任务中基于投票的方法相比，这种方法的表现一直较差（通常差距很大）。总体而言，这些结果凸显了在无验证器的情况下，当 NoThinking 方法与并行采样以及强大的选择策略相结合时的有效性。

随着 k 值的增加，NoThinking 方法在多样本准确率（pass@k）方面展现出意外的优异表现，可以通过并行 scaling 获得进一步的利用，从而在相似甚至明显更低的延迟（最多可降低至原来的九分之一）情况下，提高单样本准确率（pass@1）的结果。此外，对于配备了完美验证器的任务，这种方法还能够在保持相似或更高准确率的同时，将 token 的总使用量减少多达四分之三。

请提供要润色段落的内容，我将对其进行语言润色，提升表达质量。

大型语言模型在生成解答之前，会经历一个冗长的思考过程，这种方式在推理任务上已经取得了很好的成果。然而，该研究对这一过程的必要性提出了质疑，为此引入了NoThinking方法。

这是一种简单而有效的提示策略，能够绕过显式的思考过程。实验证明，同样的模型在没有冗长思维链的情况下，随着 pass@k 中 k 值的增加，其表现可以与显式思考方法相当，甚至优于显式思考方法，同时所使用的 token数量也要少得多。

在同等 token 预算的情况下，对于大多数的 k 值，NoThinking 方法的表现始终优于传统的 Thinking 结果。

此外，研究还发现，NoThinking 方法可以与“从 N 个中选最佳”的选择方法相结合，从而在准确率和延迟的权衡方面，取得了比标准 Thinking 方法更好的效果。

研究者表示：「我们希望这个研究能够重新激发人们对冗长思考过程的关注，强调其必要性，同时为在有限预算和低延迟情况下实现出色的推理性能提供一个极具竞争力的参考。」